2expres

Добрый день! Я могу выполнить. Ваша задача решается по крайней мере 3 способами. Нужны примеры фотографий (видео) и более точное ТЗ. Ниже пример выполненной нами задачи, определение положения человека на видео и включения над ним нужной лампы люстры (8 х 8 ламп). Слева видна таблица, какие лампы горят в данный момент. P.S. писал Вам на почту ответа нет.

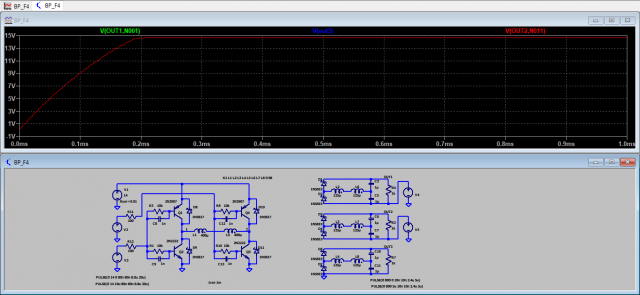
Давайте по теме.... Содержание темы не соответствует ее названию. Вместо моделирования верхних ключей моделируются низковольтные DC-DC преобразователи. Взял за основу Вашу схему, немного изменив. Результат такой же красивый, как и у Вас. Добавил паразитных емкостей 10pF. Верхние ключи погорели.

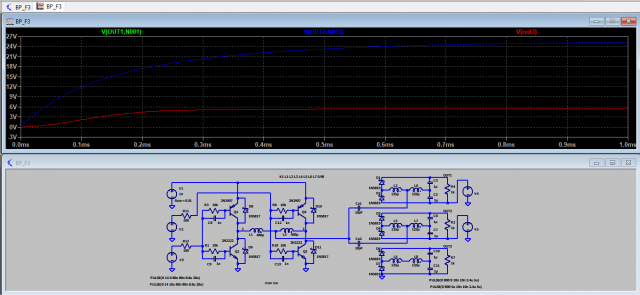
Или без контролера, генератор на 2 транзисторах, как у китайцев.

Будет, т.к. источники будут соединены с землей через источники импульсного напряжения В мостовых преобразователях и БП связаны, осциллографом я могу посмотреть напряжения друг относительно друга.

И я о том, что КПД не важен. Большее значение играет емкость между источниками. У вас в модели эти емкости отсутствуют, все они подключены к земле, а надо бы подключить к реальному высоковольтному импульсному напряжению.

Наличие резисторов R9, R10 говорит о том, что КПД вам не важен. В китайских сварочниках применяется более простая и дешевая схема генератора на двух NPN транзисторах. Это массовое производство, работа в условиях больших перепадов токов и температур.

Какие могут быть претензии к бесплатной программе? Буду пользоваться тем, что есть. Спасибо за ответы.

Вы точно знаете, что в LTspice нет способов проверки на предельно допустимые параметры? Что можно с помощью мозга, я знаю и без вас. Можно в уме моделировать и платы трассировать без ПК изолентой.

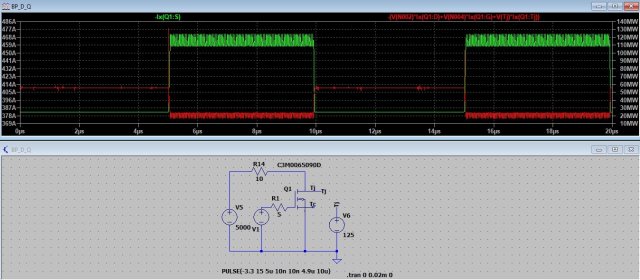
Даже очень хорошо работает, модель транзистора выдерживает токи в 460А, выделяемую на нем мощность в меговатты. Я ожидал, что должно выводится хотя бы предупреждение.

Спасибо. Установил, работает.

Здравствуйте. Если есть у кого модель SIC транзистора C3M0065090D для LTspice, поделитесь пожалуйста.

Сейчас пытаются найти применение для б/у АКБ электро автомобилей. Они не дорогие, вот для таких применений. Напряжение АКБ тоже 400В

В вашей схеме применен повышающий преобразователь для СБ. Не понятно, чем принципиально это отличается от АКБ. Тогда и для СБ нужна трансформаторная схема.

Левая часть схемы ( до Bus) замечательна. Зачем делать гальваническую развязку АБ? Почему нельзя применить три Boost для СБ, АБ и ветро генератора. Схема без применения трансформаторов, одни дроссели. Недостаток- АБ должна быть в недоступном отсеке.

Диоды нужны только для гальванических источников питания. В преобразователях уже есть как правило диоды и они соединяются напрямую. Получается общий для всех преобразователей выходной конденсатор.